In this post I want to describe my train balancing system in Factorio.
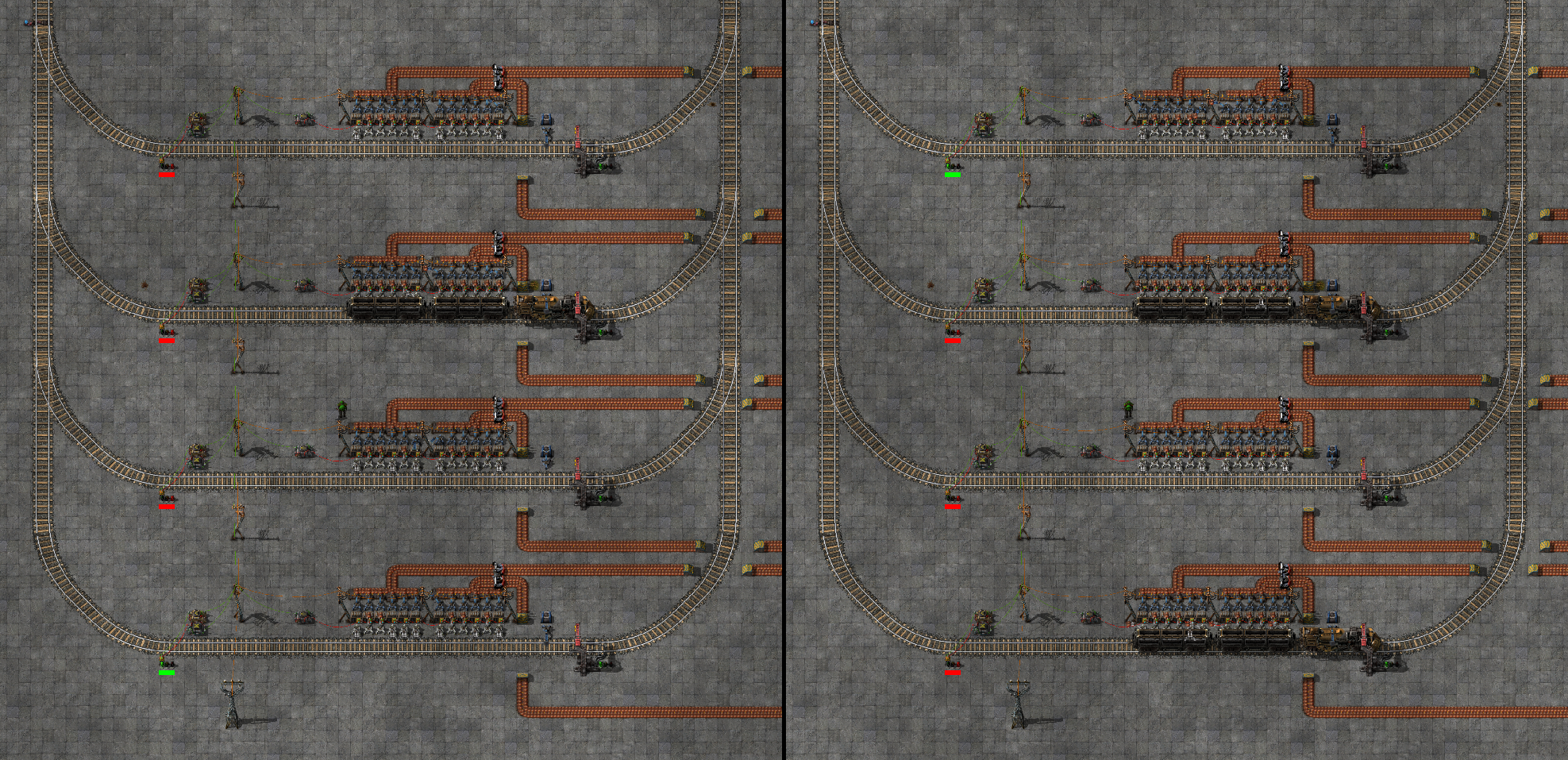
I started with a copper ore unloading station with four platforms, where all train stops had the same name. Apparently this is a lesser known fact – I could not find any documentation about it on the Factorio Wiki – but if you give a bunch of train stops the same name, the trains will choose the closest available stop. This allows you to easily create stations with multiple platforms, but in this case I had the problem that the trains would always choose the upper platform, because it is the closest to the entrance to the station on the top. This in turn caused throughput problems, because the ovens connected to the platform on the bottom would not receive any copper ore until the three platforms above were completely filled with ore and blocked by a train. Additionally, if there are less trains than platforms, even if they could supply enough ore for all platforms, they would never go to the last platform, because there would always be a free platform closer to the top and therefore closer to the train.
The solution was to add a small circuit network that controls the rail signals at the entrances to the platforms. The purpose of the circuit network is to only open the platforms that are available and have the least resources in storage. In a typical case this would only be one platform, but when the platforms are empty, they are all open.
Example
Here is a short example. On the left the fourth platform is open because it contains the least resources. The second platform is not considered because it is currently blocked by a train. As can be seen on the right, once a train arrives at the fourth platform, it is excluded from the calculation and the first platform is opened, even if it still has more resources than the fourth platform.
Construction
I will now describe how the system works in detail. This should also explain how to rebuild the circuit network.
Here is a general overview of the station. One important detail is the rail chain signal marked by a blue arrow in the top left corner. This is signal is also necessary for normal multi-platform stations. If the platform the train is currently targeting is blocked, the train will stop at this signal. If another platform gets cleared, the train can then change its target to the new platform and go there. Without this signal the train would stop directly before its target platform. If another platform got cleared, the train would have to back up a bit to go there, but trains do not go backwards in automatic mode. It would also very likely block other trains from entering the cleared platform.
Apart from the single rail chain signal, the station consists of identical platforms. One such platform is marked by a blue box and I am going to explain it in detail in the next section. The reason I am calling this a platform is because I consider the steel chests, the inserters and the circuit network components and and so on part of the platform. So the train stop and the other components together form a platform and multiple platforms form a complete station.
The platforms are connected via a green wire as indicated by the green line on the image.
Each platform is confined by two normal rail signals as indicated by the blue arrows. Also remember to give all the train stops the same name, as this is essential for the balancer to work.
The basic principle is that each platform broadcasts its current item count under a different signal on the green platform-connecting network. I used the lettered signals from the circuit network for this and for the rest of the tutorial we will be looking at platform A.
I use an EACH condition to compare the signals of the different platforms, so it is important that the green network is clean, i. e. it is only connected to the different platforms and does not carry any other signals.
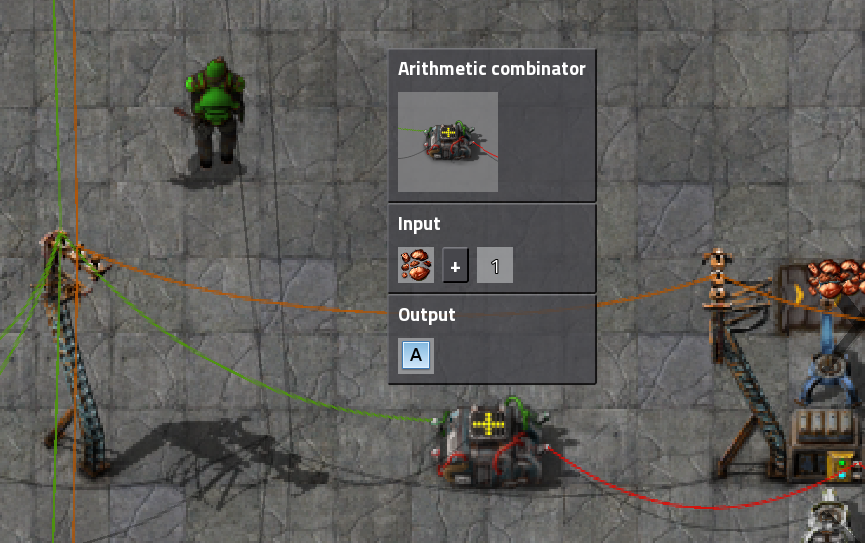
The arithmetic combinator on the right is used to publish the current item count per platform to the green network. It is connected to all the chests of the platform via the red cable. Its input is the copper ore count and its output is the signal A, so it renames the signal. But I also add 1 to the signal, because the EACH condition only works with signals that are not 0. Adding 1 guarantees that the platforms signal is always active (i. e. not 0), so that it is always picked up by the EACH condition of the other platforms, even when the current platform is empty.
The arithmetic combinator on the left adds an arbitrarily high number to the item count of the platform if it is blocked by a train. If this number is higher than the maximum storage capacity of the platform, an empty platform will always be preferred to a blocked platform. This is how the blocked platforms are excluded from the calculation.
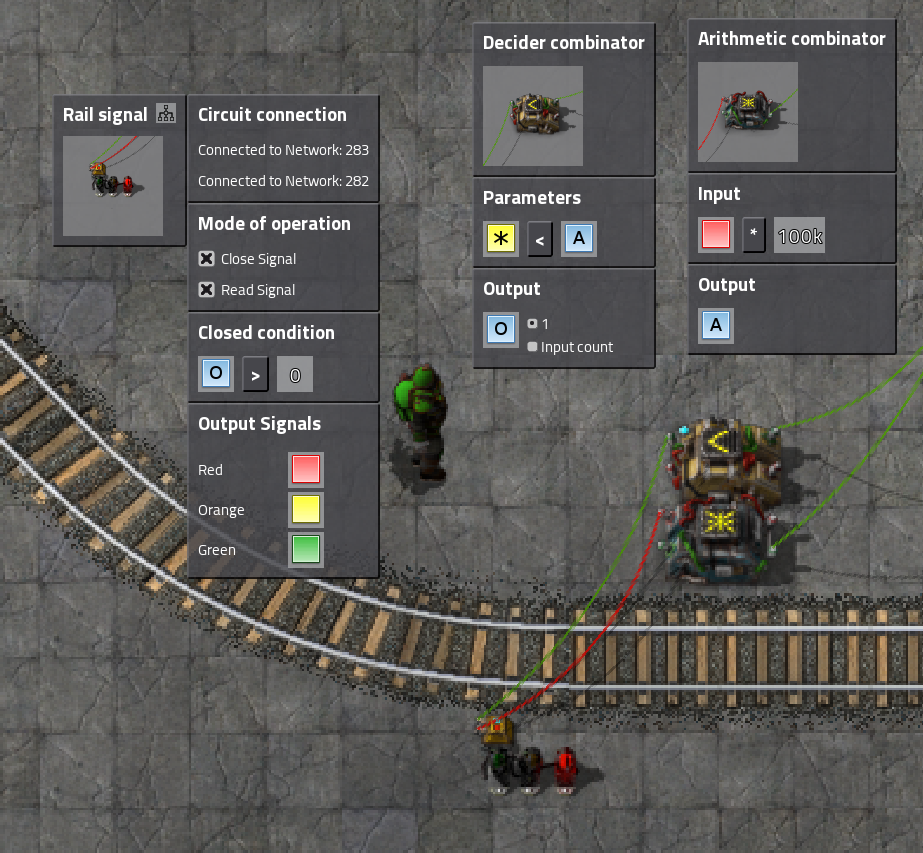
The output from the rail signal arrives via the red cable. The rail signal sends a red signal of value 1 if a train is blocking the platform. The arithmetic combinator amplifies and also renames this signal. The green circuit network then adds the outputs the two arithmetic combinators together, exactly like it adds the copper ore counts of all the connected chests.
Each platform has 12 steel chests containing 48 slots holding up to 50 copper ore each. So the total storage capacity of one platform is 12 * 48 * 50 = 28.800. So a value of 30k would be sufficient for the circuit to work, but using 100k has the nice property of being able to always see the status of the entire station just by looking at the circuit network signals. If a platforms signal is >= 100k then there is a train in that platform. On the other hand, if you ignore the 100k you get the total amount of copper ore stored within the platform (plus one, actually, because of the other arithmetic combinator, but I am assuming you do not care about that once you have 20k ore in your platforms). So 115k means 15k ore and train present, while 20k means 20k ore but no train present.
The decider combinator compares the item counts and sends the result to the rail signal. The EACH condition compares each signal independently, so in this case it would check A < A, B < A, C < A and D < A. The first comparison is obviously not wanted, but since it is always false it does not do any harm. For each comparison that is true 1 is added to the output signal. The output is routed to the rail signal which closes if the output signal is greater than zero which means at least one of the comparisons is true. So the rail signal blocks the platform if it contains more items than at least one other platform. In other words the platform is blocked if it is not the one with the least items.
Unfortunately, you cannot put the condition directly into the rail signal, because it would also publish the red signal to the station network thus messing up the EACH conditions of the other platforms.
We also need to configure the rail signal to read the signal. As the tooltip for this mode of operation will tell you, if the signal is closed because of the circuit condition, it does not output anything. This is crucial, as it prevents feedback loops.
Conclusion
I hope you found this interesting and that my instructions are understandable. For comments head over to the discussion on reddit.
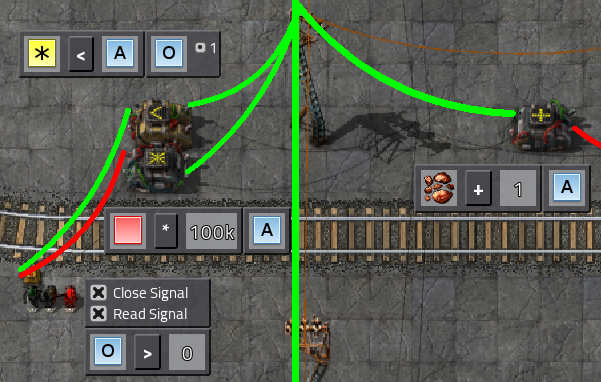
Finally, here is a quick build reference, containing the important settings of all machines in a single image.
EDIT: Thanks to /u/Yoyobuae on reddit for pointing out the EACH signal to me. This significantly reduces the number of combinators needed, so I updated the article to only show the improved design.